Transformer
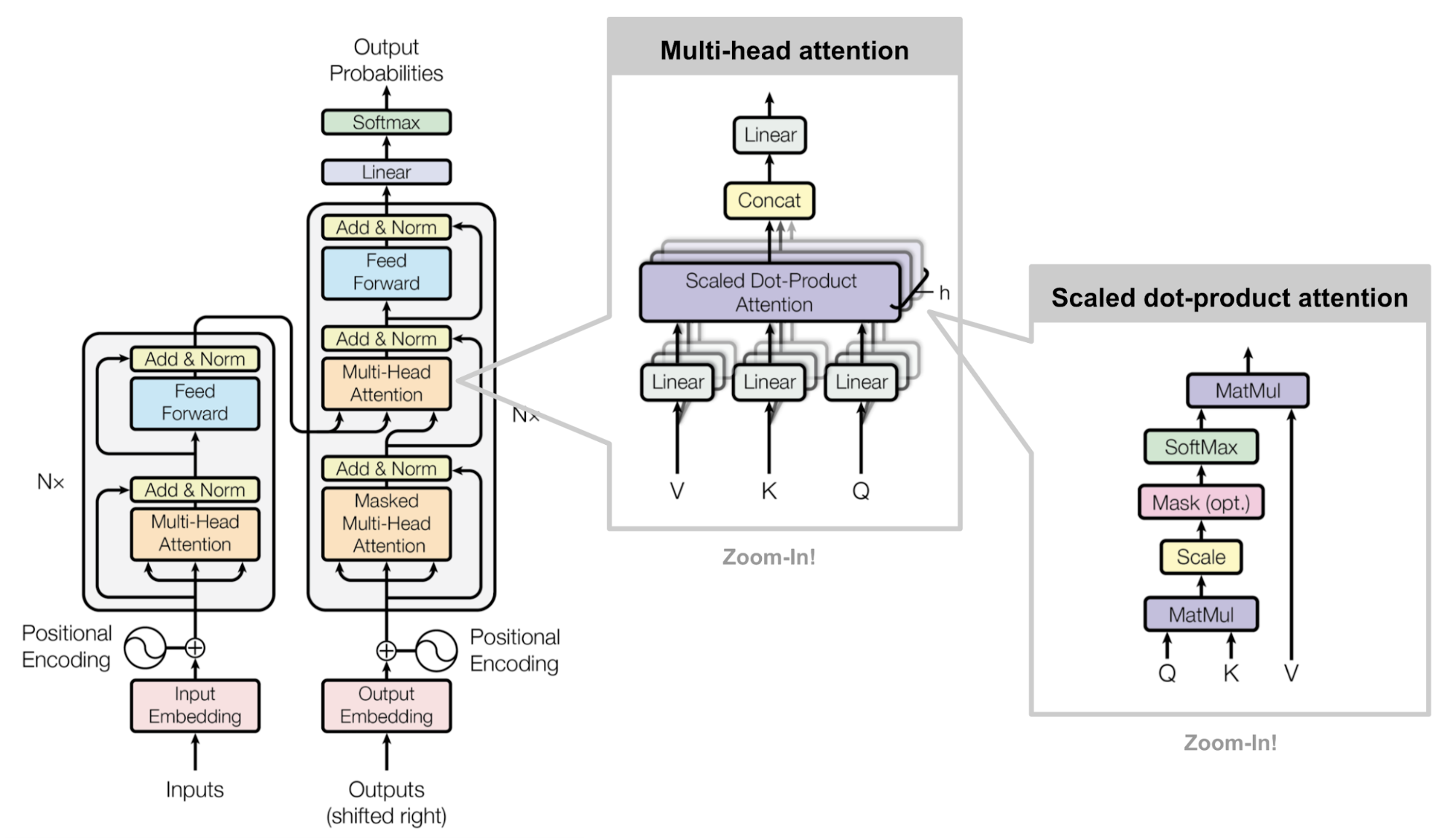
The full model architecture of the transformer.[3]
“Attention is All you Need” (Vaswani, et al., 2017), without a doubt, is one of the most impactful and interesting paper in 2017. It presented a lot of improvements to the soft attention and make it possible to do seq2seq modeling without recurrent network units. The proposed “transformer” model is entirely built on the self-attention mechanisms without using sequence-aligned recurrent architecture.
The secret recipe is carried in its model architecture.
Key, Value and Query
The major component in the transformer is the unit of multi-head self-attention mechanism. The transformer views the encoded representation of the input as a set of key-value pairs, \((\mathbf{K}, \mathbf{V})\), both of dimension \(n\) (input sequence length); in the context of NMT, both the keys and values are the encoder hidden states. In the decoder, the previous output is compressed into a query (\(\mathbf{Q}\) of dimension \(m\)) and the next output is produced by mapping this query and the set of keys and values.
The transformer adopts the scaled dot-product attention: the output is a weighted sum of the values, where the weight assigned to each value is determined by the dot-product of the query with all the keys: \[\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}\left( \frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{n}}\right) \mathbf{V}\]
Multi-Head Self-Attention
Rather than only computing the attention once, the multi-head mechanism runs through the scaled dot-product attention multiple times in parallel. The independent attention outputs are simply concatenated and linearly transformed into the expected dimensions. I assume the motivation is because ensembling always helps? ;) According to the paper, “multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.” \[\begin{align} \text{MultiHead}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) & = [\text{head}_1; ...; \text{head}_h]\mathbf{W}^O \\ \text{where head_i} & = \text{Attention}(\mathbf{QW}_i^Q, \mathbf{KW}_i^K, \mathbf{VW}_i^V) \end{align}\]
where \(\mathbf{W}_i^Q\), \(\mathbf{W}_i^K\), \(\mathbf{W}_i^V\) and \(\mathbf{W}_i^O\) are parameter matrices to be learned.
Encoder
The encoder generates an attention-based representation with capability to locate a specific piece of information from a potentially infinitely-large context.
- A stack of \(N=6\) identical layers.
- Each layer has a multi-head self-attention layer and a simple position-wise fully connected feed-forward network.
- Each sub-layer adopts a residual connection and a layer normalization. All the sub-layers output data of the same dimension \(d_\text{model} = 512\).
Decoder
The decoder is able to retrieval from the encoded representation.
- A stack of N = 6 identical layers
- Each layer has two sub-layers of multi-head attention mechanisms and one sub-layer of fully-connected feed-forward network.
- Similar to the encoder, each sub-layer adopts a residual connection and a layer normalization.
- The first multi-head attention sub-layer is modified to prevent positions from attending to subsequent positions, as we don’t want to look into the future of the target sequence when predicting the current position.
Full Architecture
Finally here is the complete view of the transformer’s architecture:
- Both the source and target sequences first go through embedding layers to produce data of the same dimension \(d_\text{model} = 512\).
- To preserve the position information, a sinusoid-wave-based positional encoding is applied and summed with the embedding output.
- A softmax and linear layer are added to the final decoder output.
Reference
[1] Lil’Log: Attention? Attention!
